琥珀色呑んだくれ備忘録

メモとか備忘録とか

Rで最長共通部分文字列を取り出す

やりたかったこと

与えられた文字列に共通する部分文字列を取り出したい。PTXQCというパッケージにLCSn()というツールが容易されている。

CRAN - Package PTXQC

install.packages("PTXQC", dependencies = TRUE)

PTXQC::LCSn(c("AAAAACBBBBB", "AAAAADBBBBB", "AAAABBBBBEF")) 
> [1] "BBBBB"

問題の名前

最長共通部分文字列（Longest common substrings; LCS）、とよばれる古典的な問題らしい。最長共通部分列（Longest common subsequence）と呼ばれるよく似た問題も同じLCSなので、メモしておかないと忘れる。

 

Longest common substrings

qiita.com

Longest common subsequence qiita.com

Rで作成した図表を「パワポでくれ」と言われた時の対処法

R R package

2020年9月7日現在、GitHub版ではofficer関連の対応がされたようだ。

niszetさん（id:niszet）から、コメントで教えていただいた。

GitHub上のexportパッケージをインストールしてコードを一式流してみたのですが、現時点(2020/Sep/06）では一通りコードが動くことを確認しました。 table2*** 関数の内部で使用している、flextableパッケージ起因の警告が出ていますが、それ以外は期待した動作をしていると思います。

また、broom::tidy(iris3)も警告は出ますが値が表示されるようです。

rglがpngのみサポートしている、は状況変わらずです（rglパッケージ自身がpngのみ対応している）

セットアップ

CRANは相変わらず凍結中なので、GitHubから最新のバージョンをインストールする。

github.com

install.packages("officer")
install.packages("rvg")
install.packages("openxlsx")
install.packages("ggplot2")
install.packages("flextable")
install.packages("xtable")
install.packages("rgl")
install.packages("stargazer")
install.packages("tikzDevice")
install.packages("xml2")
install.packages("broom")
install.packages("devtools")
library(devtools)
devtools::install_github("tomwenseleers/export")

パワポにする

基本的には、exportパッケージが提供する関数に、何も考えずにオブジェクトを放り込むだけ。

描画オブジェクトを Microsoft PowerPointにエクスポート

直前にプロットした描画オブジェクトをPowerPointに埋め込むことができる。ファイル名を指定しないとRplot.pptxという名前で出力される。

ggp <- iris %>% 
  ggplot(aes(x = Sepal.Length, y = Sepal.Width, colour = Species)) +
  geom_point()

ggp

f:id:kato-satoshi-0:20191219143749p:plain

graph2ppt()
>  Exported graph as Rplot.pptx

ベクター形式で出力されるため、PowerPointで開いて［グループ化］から解除⇔再グループ化が可能。

f:id:kato-satoshi-0:20191219144226p:plain

ggplotでなくてもOK。

plot(Sepal.Length ~ Sepal.Width, data = iris)

f:id:kato-satoshi-0:20191219144029p:plain

graph2ppt()
>  Exported graph as Rplot.pptx

f:id:kato-satoshi-0:20191219144650p:plain

直前に描画したものでなくても、描画オブジェクトが残っていれば出力できる。

ggp + geom_line() # ラインを追加描画
graph2ppt(ggp)    # ラインを追加描画していないプロットがエクスポートされる
>  Exported graph as Rplot.pptx

（イメージ省略）

スライドの追加

同じ出力ファイル名を指定して、append = TRUEを指定することで、次のスライドとして追記することができるのでfor()などを使って、一度に多量のスライドを作成することもできる。

注意点は、

  • 指定したファイルを開いたままにすると出力に失敗する*1
  • append = TRUEを指定しないと、同名のファイルに上書きされてしまう
for (sp in unique(iris$Species)) {
  ggp <- iris %>% 
    filter(Species == sp) %>% 
    ggplot(aes(x = Sepal.Length, y = Sepal.Width, colour = Petal.Length)) +
    geom_point() +
    labs(title = sp)
  
  graph2ppt(ggp, file = "./my_plot.pptx", append = TRUE)
  
}
>  Exported graph as ./my_plot.pptx
>  Exported graph as ./my_plot.pptx
>  Exported graph as ./my_plot.pptx

f:id:kato-satoshi-0:20191219145532p:plain

データフレームをPowerPointにエクスポート

データフレームの先頭の数件を表としてスライドに埋め込んでみる。全件埋め込むと、たいていの場合はひどいことになるので要注意。

iris %>% head() %>% table2ppt(append = TRUE)
>  Exported table as Rtable.pptx

（イメージ省略）

プロットとサマリーを組み合わせたスライドとかが便利そう。

ggp <- iris %>% 
  ggplot(aes(y = Sepal.Width, x =  Sepal.Length, color = Species)) +
  geom_point() + 
  geom_smooth(method=lm) 
graph2ppt(ggp, file = "./iris.pptx")
>  Exported graph as ./iris.pptx

tbl <- iris %>%
    group_by(Species) %>%
    group_modify(~ broom::tidy(lm(Sepal.Width ~ Sepal.Length, data = .x))) %>%
  table2ppt(file = "./iris.pptx", append = TRUE)
>  Exported table as ./iris.pptx

f:id:kato-satoshi-0:20191219145956p:plain

その他のオブジェクトをPowerPointにエクスポート

summary.lm()やsummary.lm()なども直接放り込めば表にしてくれる。*2 一部のオブジェクトはadd.rownames = TRUEを指定して、行名を明示的に取り込む必要があるので注意。

fit <- lm(Sepal.Width ~ Sepal.Length, data = iris)
x <- summary(fit)
tbl <- table2ppt(x = x, file = "./iris_ggplot.pptx", add.rownames = TRUE, append = TRUE)
>  Exported table as ./iris_ggplot.pptx

（イメージ省略）

その他のエクスポート

MS Office以外の出力にも充実しているので、好きなファイル形式にお任せで出力したいときには良いのでは。　

作図データのエクスポート

f:id:kato-satoshi-0:20191219150526p:plain

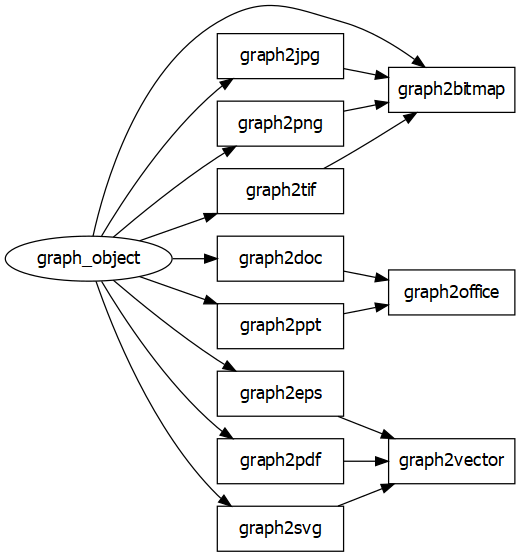
graph2office()は、オプションで様々な調整ができるが、代表的なものだけ紹介。

  • aspectr　アスペクト比の調整
  • orient　用紙の縦横向きの指定（"auto", "portrait", "landscape"）
  • upscale　TRUEを指定すると用紙いっぱいになるまでプロットを拡大する

表データのエクスポート

data.frameをはじめとして、xtable::xtable()とbroom::tidy()でサポートされているオブジェクトを出力できる。ファイル名を指定しない場合、Rtable＋拡張子というファイルが作られる。

f:id:kato-satoshi-0:20191219150610p:plain

Excelへのエクスポート

table2excel()はopenxlsxパッケージの機能をコンパクトにまとめてくれている。loadWorkbook()またはcreateWorkbook() → addWorksheet() → createStyle() → writeData() → addStyle() → saveWorkbook()をしなくていいので、お手軽でいい。

エクセルは同一ファイル内で同名のシートを許さないので、append = TRUEでシートを追加しようとするとエラーになる。

f:id:kato-satoshi-0:20191219165944p:plain

tbl <- table2excel(iris, "./my_table.xlsx")
>  Exported table as ./my_table.xlsx
tbl <- table2excel(iris, "./my_table.xlsx", append = TRUE)
>  Error in addWorksheet(doc, sheetName = sheetName): A worksheet by that name already exists! Sheet names must be unique case-insensitive.

シートを追加したい場合はsheetNameオプションをつかって、重複しないようにシート名をつけてやればよい。

sheet_index = 2
tbl <- table2excel(iris, "./my_table.xlsx", append = TRUE, sheetName = paste("sheet", sheet_index))
>  Exported table as ./my_table.xlsx

f:id:kato-satoshi-0:20191219151002p:plain

table2csv()はwrite.csv()でもよさそうに思うが、lmなどの各種オブジェクトをわざわざ自分でテーブル形式にしなくてもdata.frameを返してくれるので、一時ファイルの保存機能付きお手軽コンバータとしても使える？かも。

fit <- lm(yield ~ block + N * P + K, npk)
x <- summary(fit)
tbl <- table2csv(x)
>  Exported table as Rtable.csv
tbl %>% str
>  'data.frame':  10 obs. of  4 variables:
>   $ Estimate  : num  52.86 3.42 6.75 -3.9 -3.5 ...
>   $ Std. Error: num  2.55 2.8 2.8 2.8 2.8 2.8 2.28 2.28 1.61 3.23
>   $ t value   : num  20.71 1.22 2.41 -1.39 -1.25 ...
>   $ Pr(>|t|)  : chr  "<0.01" "0.24" "0.03" "0.18" ...
>   - attr(*, "align")= chr  "r" "r" "r" "r" ...
>   - attr(*, "digits")= num  NA 2 2 2 NA
>   - attr(*, "display")= chr  "s" "f" "f" "f" ...

また、多彩なオブジェクトに対応しているのだが、あくまでxtable::xtable()とbroom::tidy()が扱えるものに限られるため、例えばarray には対応してなかったりする。

table2excel(iris3)
>  Error in table2spreadsheet(..., type = "XLS"): array is currently not supported by table2office
xtable::xtable(iris3)
>  Error in UseMethod("xtable"):  'xtable' をクラス "c('array', 'double', 'numeric')" のオブジェクトに適用できるようなメソッドがありません
broom::tidy(iris3)
>  Error: All columns in a tibble must be 1d or 2d objects:
>  * Column `x` is array

Word／PowerPointへのエクスポート

table2doc()とtable2ppt()も内部ではflextableに渡すための面倒な調整をやっている。素直に恩恵にあずかりたい。

rgl 3Dオブジェクトのエクスポート

rglパッケージが出力する3DプロットをPNGで保存する。現在のバージョンではPNG形式しかサポートしていない。サンプルコードはあるものの、(いまではPNGもサポートされていない)https://stackoverflow.com/questions/4543272/rgl-snapshot-no-longer-worksらしい

# Create a file name
filen <- tempfile(pattern = "rgl") # or 
# filen <- paste("YOUR_DIR/rgl")

# Generate a 3D plot using 'rgl'
x = y = seq(-10, 10, length = 20)
z = outer(x, y, function(x, y) x^2 + y^2)
rgl::persp3d(x, y, z, col = 'lightblue')

# Save the plot as a png
rgl2png(file = "temp.png")

*1:結果を確認しようとして、よくやってしまいがち

*2:実際にはxtableかbroom::tidyがテーブルに変換している

XGBoostExplainerが何をやっているか調べる（４．モデルから予測ルールを抽出する）

R R package interpretability xgboost

目的

今回は、xgboostExplainerによって、xgboostの学習済みモデルからルールがどうやって抽出されているかにフォーカスし、適宜xgboostの資料を見ながら追いかける。

（参考資料）

関連シリーズ

  1. とりあえず使ってみる
  2. 予測結果の可視化プロセスをstep-by-stepで実行する
  3. 予測結果を分解再構成するプロセスをstep-by-stepで実行する
  4. 学習したxgboostのルール抽出をstep-by-stepで実行する（この記事）

準備：XGBモデルの学習と予測

xgboostExplainerのマニュアルにあるexampleからコピペ。

require(tidyverse)
library(xgboost)
library(xgboostExplainer)

set.seed(123)

data(agaricus.train, package='xgboost')

X = as.matrix(agaricus.train$data)
y = agaricus.train$label
table(y)
train_idx = 1:5000

train.data = X[train_idx,]
test.data = X[-train_idx,]

xgb.train.data <- xgb.DMatrix(train.data, label = y[train_idx])
xgb.test.data <- xgb.DMatrix(test.data)

param <- list(objective = "binary:logistic")
xgb.model <- xgboost(param =param,  data = xgb.train.data, nrounds=3)

学習したxgboostのルール抽出

buildExplainer()の中身を抜き書きしながら、step-by-stepで眺める

# explainer = buildExplainer(xgb.model,xgb.train.data, type="binary", base_score = 0.5, trees = NULL)
# function (xgb.model, trainingData, type = "binary", base_score = 0.5, trees_idx = NULL) 
# {
trainingData = xgb.train.data
type = "binary" 
base_score = 0.5
trees_idx = NULL

xgb.model.dt.tree()によるパスの抽出

xgboost::xgb.model.dt.tree()を使う。

col_names = attr(trainingData, ".Dimnames")[[2]]
col_names %>% head()
#> [1] "cap-shape=bell"    "cap-shape=conical" "cap-shape=convex" 
#> [4] "cap-shape=flat"    "cap-shape=knobbed" "cap-shape=sunken"

cat("\nCreating the trees of the xgboost model...")
#> 
#> Creating the trees of the xgboost model...
trees = xgb.model.dt.tree(col_names, model = xgb.model, trees = trees_idx)

trees %>% 
  mutate(Feature = str_trunc(Feature, width=12, side="left")) %>% 
  select(-Missing)
#>    Tree Node   ID      Feature Split  Yes   No      Quality       Cover
#> 1     0    0  0-0    odor=foul   0.5  0-1  0-2 2711.3557100 1250.000000
#> 2     0    1  0-1 ...ize=broad   0.5  0-3  0-4 1263.3979500  901.000000
#> 3     0    2  0-2         Leaf    NA <NA> <NA>    0.5982857  349.000000
#> 4     0    3  0-3    odor=none   0.5  0-5  0-6  264.4693910  202.250000
#> 5     0    4  0-4 ...lor=green   0.5  0-7  0-8  203.9635310  698.750000
#> 6     0    5  0-5 ...or=yellow   0.5  0-9 0-10  121.6305770  157.500000
#> 7     0    6  0-6 ...ing=silky   0.5 0-11 0-12   74.7532349   44.750000
#> 8     0    7  0-7         Leaf    NA <NA> <NA>   -0.5991260  685.500000
#> 9     0    8  0-8         Leaf    NA <NA> <NA>    0.5578948   13.250000
#> 10    0    9  0-9  odor=almond   0.5 0-13 0-14   65.5069656  148.000000
#> 11    0   10 0-10         Leaf    NA <NA> <NA>   -0.5428572    9.500000
#> 12    0   11 0-11 ...?=bruises   0.5 0-15 0-16   26.8929482   38.250000
#> 13    0   12 0-12         Leaf    NA <NA> <NA>    0.5200000    6.500000
#> 14    0   13 0-13   odor=anise   0.5 0-17 0-18   62.2878838  143.250000
#> 15    0   14 0-14         Leaf    NA <NA> <NA>   -0.4956522    4.750000
#> 16    0   15 0-15         Leaf    NA <NA> <NA>   -0.5838926   36.250000
#> 17    0   16 0-16         Leaf    NA <NA> <NA>    0.4000000    2.000000
#> 18    0   17 0-17         Leaf    NA <NA> <NA>    0.5957143  139.000000
#> 19    0   18 0-18         Leaf    NA <NA> <NA>   -0.4857143    4.250000
#> 20    1    0  1-0    odor=foul   0.5  1-1  1-2 1489.0952100 1145.302000
#> 21    1    1  1-1 ...ize=broad   0.5  1-3  1-4  691.4842530  825.759888
#> 22    1    2  1-2         Leaf    NA <NA> <NA>    0.4634756  319.542114
#> 23    1    3  1-3    odor=none   0.5  1-5  1-6  142.5185550  186.003708
#> 24    1    4  1-4 ...lor=green   0.5  1-7  1-8  114.8126300  639.756165
#> 25    1    5  1-5  odor=almond   0.5  1-9 1-10   69.8917542  144.674194
#> 26    1    6  1-6 ...ing=silky   0.5 1-11 1-12   42.7613907   41.329517
#> 27    1    7  1-7         Leaf    NA <NA> <NA>   -0.4640480  627.485962
#> 28    1    8  1-8         Leaf    NA <NA> <NA>    0.4361763   12.270212
#> 29    1    9  1-9   odor=anise   0.5 1-13 1-14   75.4965286  135.787827
#> 30    1   10 1-10         Leaf    NA <NA> <NA>   -0.4301576    8.886355
#> 31    1   11 1-11 ...?=bruises   0.5 1-15 1-16   16.6019783   35.249847
#> 32    1   12 1-12         Leaf    NA <NA> <NA>    0.4107886    6.079669
#> 33    1   13 1-13         Leaf    NA <NA> <NA>    0.4617254  127.362411
#> 34    1   14 1-14         Leaf    NA <NA> <NA>   -0.4283619    8.425421
#> 35    1   15 1-15         Leaf    NA <NA> <NA>   -0.4537036   33.327763
#> 36    1   16 1-16         Leaf    NA <NA> <NA>    0.3296103    1.922086
#> 37    2    0  2-0    odor=foul   0.5  2-1  2-2  934.9316410  956.514771
#> 38    2    1  2-1 ...ize=broad   0.5  2-3  2-4  434.1681820  689.965515
#> 39    2    2  2-2         Leaf    NA <NA> <NA>    0.4022448  266.549286
#> 40    2    3  2-3    odor=none   0.5  2-5  2-6   87.7709885  156.324432
#> 41    2    4  2-4 ...lor=green   0.5  2-7  2-8   73.6840591  533.641052
#> 42    2    5  2-5  odor=almond   0.5  2-9 2-10   44.8767204  121.285667
#> 43    2    6  2-6 ...ing=silky   0.5 2-11 2-12   27.4686470   35.038773
#> 44    2    7  2-7         Leaf    NA <NA> <NA>   -0.4028375  523.192078
#> 45    2    8  2-8         Leaf    NA <NA> <NA>    0.3751199   10.448951
#> 46    2    9  2-9   odor=anise   0.5 2-13 2-14   48.7504120  113.642014
#> 47    2   10 2-10         Leaf    NA <NA> <NA>   -0.3680061    7.643652
#> 48    2   11 2-11 ...?=bruises   0.5 2-15 2-16   11.4850969   29.765743
#> 49    2   12 2-12         Leaf    NA <NA> <NA>    0.3515948    5.273030
#> 50    2   13 2-13         Leaf    NA <NA> <NA>    0.4004391  106.384308
#> 51    2   14 2-14         Leaf    NA <NA> <NA>   -0.3663105    7.257702
#> 52    2   15 2-15         Leaf    NA <NA> <NA>   -0.3922864   28.009958
#> 53    2   16 2-16         Leaf    NA <NA> <NA>    0.2832851    1.755784
# %>%
#   mutate_at(.vars = vars("Quality","Cover"), .funs = round)

「LeafノードのQualityは0じゃないの？」と思うかもしれないが、マニュアルに

Quality: either the split gain (change in loss) or the leaf value

と書いてあり、LeafノードではQualityのセルが予測結果の格納場所として流用されていることに注意。（あとからこれを利用する）*1

cat("\nGetting the leaf nodes for the training set observations...")
#> 
#> Getting the leaf nodes for the training set observations...

なお、関数内で呼ばれているpredict(..., predleaf = TRUE)は、predleaf = TRUEを指定することで、予測値の代わりに訓練データのインスタンスが各treeで所属するLeafのノード番号を取得できる。 今回はNROW(trainingData)=5000, nrounds = 3なので、5000行3列の所属Leafの行列が得られる。

nodes.train %>% dim()
#> [1] 5000    3
nodes.train <- NULL

ただし、取得されたのち削除しても特に問題はなく、学習に使われたインスタンスの予測結果の情報が、buildExplainer()のどこかで使われている形跡は見当たらなかった*2。

予測値の再分配

xgboostExplainerは、Leafの予測値を親ノードに再分配することで、予測結果を各ノードにおけるImpactとして分解し、そこを通るインスタンスの予測結果を説明する。

以下では、buildExplainer()のエンジン部分であるxgboostExplainer:::getStatsForTrees()の一連のステップをトレースする。

# tree_list = xgboostExplainer:::getStatsForTrees(trees, nodes.train, type = type, base_score = base_score)
# function (trees, nodes.train, type = "binary", base_score = 0.5) 
# {

なお、関数内部でdata.table::copy()'により、- attr(*, ".internal.selfref")=`で、データの更新が参照渡しとして行われているのに注意*3。

tree_datatable = data.table::copy(trees)

Cover (H)の再計算

xgb.model.dt.tree()の情報から、各ノードまでの二次の勾配の和を取り出す。これはCover列の情報そのもののはずなのだが、xgb.model.dt.tree()の出力するCoverは精度に問題がある*4とのことで、きちんととした精度で計算しなおす。

f:id:kato-satoshi-0:20181231135410p:plain:w480

LeafノードのCoverから、逆向きにたどりながら足し合わせていけばよい

type = "binary"
base_score = 0.5

tree_datatable[, leaf := (Feature == "Leaf")]
non.leaves = which(tree_datatable[, leaf] == F)

tree_datatable[, H := Cover]

cat("\n\nRecalculating the cover for each non-leaf... \n")
#> 
#> 
#> Recalculating the cover for each non-leaf...
print.counter = 1
for (i in rev(non.leaves)) {
  left = tree_datatable[i, Yes]
  right = tree_datatable[i, No]
  
  tree_datatable[i, H := (tree_datatable[ID == left, H] + 
                            tree_datatable[ID == right, H])]
  
  if(print.counter < 5){
    print(i - 1)
    
    bind_rows(tree_datatable[i, ],
              tree_datatable[ID == left, ], 
              tree_datatable[ID == right,]) %>% 
      select(-Tree,-Node,-Feature,-Split,-Missing) %>% 
      print()
    print.counter <- print.counter + 1
  }
}
#> [1] 47
#>      ID  Yes   No    Quality     Cover  leaf         H
#> 1: 2-11 2-15 2-16 11.4850969 29.765743 FALSE 29.765742
#> 2: 2-15 <NA> <NA> -0.3922864 28.009958  TRUE 28.009958
#> 3: 2-16 <NA> <NA>  0.2832851  1.755784  TRUE  1.755784
#> [1] 45
#>      ID  Yes   No    Quality      Cover  leaf          H
#> 1:  2-9 2-13 2-14 48.7504120 113.642014 FALSE 113.642010
#> 2: 2-13 <NA> <NA>  0.4004391 106.384308  TRUE 106.384308
#> 3: 2-14 <NA> <NA> -0.3663105   7.257702  TRUE   7.257702
#> [1] 42
#>      ID  Yes   No    Quality    Cover  leaf        H
#> 1:  2-6 2-11 2-12 27.4686470 35.03877 FALSE 35.03877
#> 2: 2-11 2-15 2-16 11.4850969 29.76574 FALSE 29.76574
#> 3: 2-12 <NA> <NA>  0.3515948  5.27303  TRUE  5.27303
#> [1] 41
#>      ID  Yes   No    Quality      Cover  leaf          H
#> 1:  2-5  2-9 2-10 44.8767204 121.285667 FALSE 121.285663
#> 2:  2-9 2-13 2-14 48.7504120 113.642014 FALSE 113.642010
#> 3: 2-10 <NA> <NA> -0.3680061   7.643652  TRUE   7.643652

CoverとHを比べてみると、たしかに足し算の結果がずれている..。

勾配(G)とweightの再分配

xgboost::xgb.model.dt.tree()の出力のうち、LeafノードではQualityのセルが予測結果の格納場所として流用されているので、これを起点にして、各親ノードにweightを再分配する。

定義上、 w^*_j=-\frac{G_j}{H_j+\lambda} なのだが、これ以降 \lambdaが入っていないので、G_j = \sum_{i \in I_j}^{} g_i とは厳密な意味では違うのかもしれないが、ここは読み取れなかった。

base_weight = log(base_score/(1 - base_score))

tree_datatable[, previous_weight := base_weight]
tree_datatable[1, previous_weight:=0]

tree_datatable[leaf==T, weight := base_weight + Quality]

tree_datatable[leaf==T, G := -weight * H]

以降は、round(Tree)単位に分けて処理を進める。

tree_list = split(tree_datatable,as.factor(tree_datatable$Tree))
tree_list %>% str(1)
#> List of 3
#>  $ 0:Classes 'data.table' and 'data.frame':  19 obs. of  15 variables:
#>   ..- attr(*, ".internal.selfref")=<externalptr> 
#>  $ 1:Classes 'data.table' and 'data.frame':  17 obs. of  15 variables:
#>   ..- attr(*, ".internal.selfref")=<externalptr> 
#>  $ 2:Classes 'data.table' and 'data.frame':  17 obs. of  15 variables:
#>   ..- attr(*, ".internal.selfref")=<externalptr>

各roundのLeaf以外の親ノードjの G_jを計算する。定義から、 I_j = I_{left, j}+I_{right, j} なので、 G_j = \sum_{i \in I_{left,j}}^{} g_i + \sum_{i \in I_{right,j}}^{} g_i = G_{L,j} + G_{R,j} の足し算を計算すればよい*5。

f:id:kato-satoshi-0:20181231140712p:plain:w480

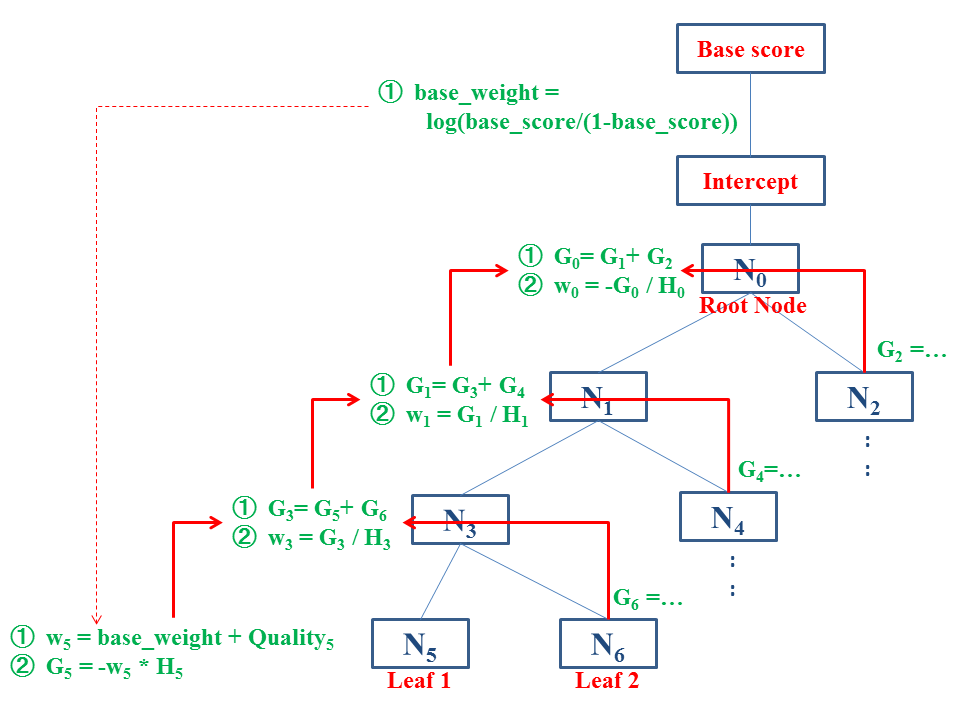
num_tree_list = length(tree_list)
treenums =  as.character(0:(num_tree_list-1))
t = 0
cat('\n\nFinding the stats for the xgboost trees...\n')
#> 
#> 
#> Finding the stats for the xgboost trees...
# pb <- txtProgressBar(style=3)
for (tree in tree_list){
  t=t+1
  num_nodes = nrow(tree)
  non_leaf_rows = rev(which(tree[,leaf]==F))
  for (r in non_leaf_rows){
    left = tree[r,Yes]
    right = tree[r,No]
    leftG = tree[ID==left,G]
    rightG = tree[ID==right,G]
    
    tree[r,G:=leftG+rightG]
    w=tree[r,-G/H]
    
    tree[r,weight:=w]
    tree[ID==left,previous_weight:=w]
    tree[ID==right,previous_weight:=w]
    
    # bind_rows(tree[r,], tree[ID==left,], tree[ID==right,]) %>% print()
  }
  
  tree[,uplift_weight:=weight-previous_weight]
  # setTxtProgressBar(pb, t / num_tree_list)
}

tree_list %>% str(1)
#> List of 3
#>  $ 0:Classes 'data.table' and 'data.frame':  19 obs. of  16 variables:
#>   ..- attr(*, ".internal.selfref")=<externalptr> 
#>   ..- attr(*, "index")= int(0) 
#>   .. ..- attr(*, "__ID")= int [1:19] 1 2 11 12 13 14 15 16 17 18 ...
#>  $ 1:Classes 'data.table' and 'data.frame':  17 obs. of  16 variables:
#>   ..- attr(*, ".internal.selfref")=<externalptr> 
#>   ..- attr(*, "index")= int(0) 
#>   .. ..- attr(*, "__ID")= int [1:17] 1 2 11 12 13 14 15 16 17 3 ...
#>  $ 2:Classes 'data.table' and 'data.frame':  17 obs. of  16 variables:
#>   ..- attr(*, ".internal.selfref")=<externalptr> 
#>   ..- attr(*, "index")= int(0) 
#>   .. ..- attr(*, "__ID")= int [1:17] 1 2 11 12 13 14 15 16 17 3 ...

各ルールのインパクトの集計（Tree Breakdown）

buildExplainerFromTreeList()を実行すると、

  • 各treeでgetTreeBreakdown()が呼ばれ、
    • 各LeafでgetLeafBreakdown()が呼ばれ、
      • findPath()がLeaf → root node までのパスを取得
      • Leaf → root nodeまでのupliftに基づいて、各パスのImpactを集計
      • root nodeのupliftをInterceptとする

f:id:kato-satoshi-0:20181231140052p:plain:w480

upliftの計算自体は、weightの再分配の際にいっしょに処理されている。

#> STEP 2 of 2
explainer = xgboostExplainer:::buildExplainerFromTreeList(tree_list, col_names)
#> 
#> 
#> Getting breakdown for each leaf of each tree...
#> 
  |=================================================================| 100%

explainer %>% str(0)
#> Classes 'data.table' and 'data.frame':   28 obs. of  129 variables:
#>  - attr(*, ".internal.selfref")=<externalptr>

本質的な部分ではないので、step-by-stepは省略。 取り出したImpactを該当列（とIntercept）に格納する。最終的には [ルール数＋１]列 ×Leaf数の行列がexplainerとして返る。 explainerの中身は以前見た通り。

kato-kohaku-0.hatenablog.com

可視化もこれまで通り。

showWaterfall(xgb.model, explainer, xgb.test.data, test.data,  2, type = "binary")
#> 
#> 
#> Extracting the breakdown of each prediction...
#> 
  |=================================================================| 100%
#> 
#> DONE!
#> 
#> Prediction:  0.811208
#> Weight:  1.457879
#> Breakdown
#>        intercept  gill-size=broad        odor=foul        odor=none 
#>      -0.27084657       1.61423045      -0.67129347       0.45408751 
#>       odor=anise      odor=almond cap-color=yellow 
#>       0.13628094       0.13073006       0.06468987

f:id:kato-satoshi-0:20181212131040p:plain

*1:論文を読んでからコードを読み進めていて、ここではまった。

*2:この実装、全般的にレガシーが残っている傾向があって、追いかけていったら途中で行き止まりだった、みたいなことが、あちこちである

*3:メモリの節約のためと思われるが、今回はトレースのため、元コードから変数名を変更した

*4:途中の丸め方に問題があるのかな

*5:論文中には、GR ← G － GLと書いてある（Algrithm.1）

XGBoostExplainerが何をやっているか調べる（３．予測結果の再構成プロセスを眺める）

R R package xgboost interpretability

目的

今回は、インスタンスの予測結果が再構成されるプロセスを、explainPredictions()の中身を抜き書きしながら、何から何が取り出されているか見ていく。

関連シリーズ

  1. とりあえず使ってみる
  2. 予測結果の可視化プロセスをstep-by-stepで実行する
  3. 予測結果を分解再構成するプロセスをstep-by-stepで実行する（この記事）
  4. 学習したxgboostのルール抽出をstep-by-stepで実行する

準備

XGBモデルの学習と予測

xgboostExplainerのマニュアルにあるexampleからコピペ。

require(tidyverse)
library(xgboost)
library(xgboostExplainer)

set.seed(123)

data(agaricus.train, package='xgboost')

X = as.matrix(agaricus.train$data)
y = agaricus.train$label
table(y)
train_idx = 1:5000

train.data = X[train_idx,]
test.data = X[-train_idx,]

xgb.train.data <- xgb.DMatrix(train.data, label = y[train_idx])
xgb.test.data <- xgb.DMatrix(test.data)

param <- list(objective = "binary:logistic")
xgb.model <- xgboost(param =param,  data = xgb.train.data, nrounds=3)

予測ルールを抽出する

buildExplainer()で、学習したxgboostのモデルから予測ルールを抽出する。

library(xgboostExplainer)

explainer = buildExplainer(xgb.model,xgb.train.data, type="binary", base_score = 0.5, trees = NULL)

予測値を再構成する

overview

指定したインスタンスの予測結果を、buildExplainer()が学習したモデルから再構成した結果(breakdown)を眺める。

再構成の大まかな手順は以下の通り：

  1. 指定したインスタンスが各roundでどのleafに落ちるか予測結果を得る
  2. 各roundで該当するleafの各特徴量の予測値への貢献量(予測ルール)を得る
  3. 2を集計し、round全体での予測ルールを得る
  4. 3を集計し、予測値を得る

対象の予測

今回は省略のため、1インスタンスだけを対象として指定するが、下記idxは複数のインスタンスを指定するベクトルでもよい。

require(data.table)
# breakdown = explainPredictions(xgb.model, explainer, slice(DMatrix, as.integer(idx)))
# function (xgb.model, explainer, data) 

DMatrix = xgb.test.data
idx = 2

data = slice(DMatrix, as.integer(idx))

nodes = predict(xgb.model, data, predleaf = TRUE)
print(nodes)
#>      [,1] [,2] [,3]
#> [1,]   17   13   13

xgboost:::predict.xgb.Booster()は、predleaf = TRUEオプションを指定することで、あるインスタンスの予測時に、それぞれのroundのtreeでどのleafに落ちたか？を返してくれる

初期化

インスタンスの数（行）× Interceptを含むすべてのルール（列）からなるゼロ行列を準備する。

colnames = names(explainer)[1:(ncol(explainer) - 2)]
  
preds_breakdown = data.table(matrix(0, nrow = nrow(nodes), ncol = length(colnames)))
setnames(preds_breakdown, colnames)
  
num_trees = ncol(nodes)

cat("\n\nExtracting the breakdown of each prediction...\n")
#> 
#> Extracting the breakdown of each prediction...

preds_breakdown.init <- preds_breakdown

対象のtreeの取り出し

今後のトレースを楽にするために「すべての行が0の列を削除し、残った列の列名を短縮する」関数を自作した。

selectNonzeroToShort <- function(data, w=12){
  select_if(data,
            .predicate = function(x){ sum(abs(x)) > 0} , 
            .funs = function(x){ str_trunc(x, width=w, side="left") }) 
}

最初のtreeだけ少し丁寧にトレースする（残りは繰り返しなので省略）

x=1

nodes_for_tree = nodes[, x]
nodes_for_tree
#> [1] 17

buildExplainer()でとりだしたLeafのうち、このroundで対象となる木のLeafを列挙。

tree_breakdown = explainer[tree == x - 1]
tree_breakdown %>% selectNonzeroToShort()
#>     ...or=yellow ...?=bruises odor=almond  odor=anise  odor=foul
#>  1:   0.00000000   0.00000000  0.00000000  0.00000000  0.7088975
#>  2:   0.00000000   0.00000000  0.00000000  0.00000000 -0.2745896
#>  3:   0.00000000   0.00000000  0.00000000  0.00000000 -0.2745896
#>  4:  -1.00780012   0.00000000  0.00000000  0.00000000 -0.2745896
#>  5:   0.00000000   0.00000000  0.00000000  0.00000000 -0.2745896
#>  6:   0.06468987   0.00000000 -1.02528500  0.00000000 -0.2745896
#>  7:   0.00000000  -0.05144537  0.00000000  0.00000000 -0.2745896
#>  8:   0.00000000   0.93244731  0.00000000  0.00000000 -0.2745896
#>  9:   0.06468987   0.00000000  0.03399723  0.03208427 -0.2745896
#> 10:   0.06468987   0.00000000  0.03399723 -1.04934438 -0.2745896
#>      odor=none ...ize=broad ...ing=silky ...lor=green  intercept leaf
#>  1:  0.0000000    0.0000000    0.0000000   0.00000000 -0.1106117    2
#>  2:  0.0000000   -0.1919848    0.0000000  -0.02193993 -0.1106117    7
#>  3:  0.0000000   -0.1919848    0.0000000   1.13508088 -0.1106117    8
#>  4:  0.1868594    0.6632849    0.0000000   0.00000000 -0.1106117   10
#>  5: -0.6576614    0.6632849    0.8995779   0.00000000 -0.1106117   12
#>  6:  0.1868594    0.6632849    0.0000000   0.00000000 -0.1106117   14
#>  7: -0.6576614    0.6632849   -0.1528694   0.00000000 -0.1106117   15
#>  8: -0.6576614    0.6632849   -0.1528694   0.00000000 -0.1106117   16
#>  9:  0.1868594    0.6632849    0.0000000   0.00000000 -0.1106117   17
#> 10:  0.1868594    0.6632849    0.0000000   0.00000000 -0.1106117   18

対象のleafのとりだし

round=1のtreeのなかのLeaf ==17が、今回の予測ルール（予測値に各特徴量が寄与する変化量）。これを取り出して、preds_breakdownに足し合わせていく。

preds_breakdown_for_tree = 
  tree_breakdown[match(nodes_for_tree, tree_breakdown$leaf), ]

print("preds_breakdown_for_tree")
#> [1] "preds_breakdown_for_tree"
preds_breakdown_for_tree %>%  
  selectNonzeroToShort(w=20) %>% 
  glimpse()
#> Observations: 1
#> Variables: 8
#> $ `cap-color=yellow` <dbl> 0.06468987
#> $ `odor=almond`      <dbl> 0.03399723
#> $ `odor=anise`       <dbl> 0.03208427
#> $ `odor=foul`        <dbl> -0.2745896
#> $ `odor=none`        <dbl> 0.1868594
#> $ `gill-size=broad`  <dbl> 0.6632849
#> $ intercept          <dbl> -0.1106117
#> $ leaf               <int> 17

preds_breakdown = 
  preds_breakdown + 
  preds_breakdown_for_tree[,colnames, with = FALSE]

print("preds_breakdown")
#> [1] "preds_breakdown"
preds_breakdown %>%  
  selectNonzeroToShort(w=20) %>% 
  glimpse()
#> Observations: 1
#> Variables: 7
#> $ `cap-color=yellow` <dbl> 0.06468987
#> $ `odor=almond`      <dbl> 0.03399723
#> $ `odor=anise`       <dbl> 0.03208427
#> $ `odor=foul`        <dbl> -0.2745896
#> $ `odor=none`        <dbl> 0.1868594
#> $ `gill-size=broad`  <dbl> 0.6632849
#> $ intercept          <dbl> -0.1106117

すべてのroudsをまとめて実行すると、以下の通り。

preds_breakdown <- preds_breakdown.init
for (x in 1:num_trees) {
  print(x)
  
  nodes_for_tree = nodes[, x]
  tree_breakdown = explainer[tree == x - 1]

  preds_breakdown_for_tree = 
    tree_breakdown[match(nodes_for_tree, tree_breakdown$leaf), ]
  
  print("preds_breakdown_for_tree")
  preds_breakdown_for_tree %>%  
    selectNonzeroToShort(w=20) %>% 
    glimpse()
  
  preds_breakdown = 
    preds_breakdown + 
    preds_breakdown_for_tree[,colnames, with = FALSE]
  
  print("preds_breakdown")
  preds_breakdown %>%  
    selectNonzeroToShort(w=20) %>% 
    glimpse()
}
#> [1] 1
#> [1] "preds_breakdown_for_tree"
#> Observations: 1
#> Variables: 8
#> $ `cap-color=yellow` <dbl> 0.06468987
#> $ `odor=almond`      <dbl> 0.03399723
#> $ `odor=anise`       <dbl> 0.03208427
#> $ `odor=foul`        <dbl> -0.2745896
#> $ `odor=none`        <dbl> 0.1868594
#> $ `gill-size=broad`  <dbl> 0.6632849
#> $ intercept          <dbl> -0.1106117
#> $ leaf               <int> 17
#> [1] "preds_breakdown"
#> Observations: 1
#> Variables: 7
#> $ `cap-color=yellow` <dbl> 0.06468987
#> $ `odor=almond`      <dbl> 0.03399723
#> $ `odor=anise`       <dbl> 0.03208427
#> $ `odor=foul`        <dbl> -0.2745896
#> $ `odor=none`        <dbl> 0.1868594
#> $ `gill-size=broad`  <dbl> 0.6632849
#> $ intercept          <dbl> -0.1106117
#> [1] 2
#> [1] "preds_breakdown_for_tree"
#> Observations: 1
#> Variables: 8
#> $ `odor=almond`     <dbl> 0.05139002
#> $ `odor=anise`      <dbl> 0.05522851
#> $ `odor=foul`       <dbl> -0.2125787
#> $ `odor=none`       <dbl> 0.1433645
#> $ `gill-size=broad` <dbl> 0.5101908
#> $ intercept         <dbl> -0.08586974
#> $ leaf              <int> 13
#> $ tree              <dbl> 1
#> [1] "preds_breakdown"
#> Observations: 1
#> Variables: 7
#> $ `cap-color=yellow` <dbl> 0.06468987
#> $ `odor=almond`      <dbl> 0.08538725
#> $ `odor=anise`       <dbl> 0.08731278
#> $ `odor=foul`        <dbl> -0.4871683
#> $ `odor=none`        <dbl> 0.3302238
#> $ `gill-size=broad`  <dbl> 1.173476
#> $ intercept          <dbl> -0.1964815
#> [1] 3
#> [1] "preds_breakdown_for_tree"
#> Observations: 1
#> Variables: 8
#> $ `odor=almond`     <dbl> 0.04534281
#> $ `odor=anise`      <dbl> 0.04896816
#> $ `odor=foul`       <dbl> -0.1841252
#> $ `odor=none`       <dbl> 0.1238637
#> $ `gill-size=broad` <dbl> 0.4407547
#> $ intercept         <dbl> -0.0743651
#> $ leaf              <int> 13
#> $ tree              <dbl> 2
#> [1] "preds_breakdown"
#> Observations: 1
#> Variables: 7
#> $ `cap-color=yellow` <dbl> 0.06468987
#> $ `odor=almond`      <dbl> 0.1307301
#> $ `odor=anise`       <dbl> 0.1362809
#> $ `odor=foul`        <dbl> -0.6712935
#> $ `odor=none`        <dbl> 0.4540875
#> $ `gill-size=broad`  <dbl> 1.61423
#> $ intercept          <dbl> -0.2708466

# return(preds_breakdown)

検算

元実装の結果と合致してるか検算。分解再構成した結果の可視化。

preds_breakdown %>% selectNonzeroToShort(w=20)
#>    cap-color=yellow odor=almond odor=anise  odor=foul odor=none
#> 1:       0.06468987   0.1307301  0.1362809 -0.6712935 0.4540875
#>    gill-size=broad  intercept
#> 1:         1.61423 -0.2708466

weight <- sum(preds_breakdown)
weight
#> [1] 1.457879

prediction <- exp(weight)/(1+exp(weight))
prediction
#> [1] 0.811208

showWaterfall(xgb.model, explainer, xgb.test.data, test.data,  2, type = "binary")
#> 
#> Extracting the breakdown of each prediction...
#>                                                                        
  |=================================================================| 100%
#> 
#> DONE!
#> 
#> Prediction:  0.811208
#> Weight:  1.457879
#> Breakdown
#>        intercept  gill-size=broad        odor=foul        odor=none 
#>      -0.27084657       1.61423045      -0.67129347       0.45408751 
#>       odor=anise      odor=almond cap-color=yellow 
#>       0.13628094       0.13073006       0.06468987

f:id:kato-satoshi-0:20181212131040p:plain

次回は、buildExplainer()が、どのような手続きで学習したxgboostのモデルから予測ルールを抽出しているのか詳細に見ていく。

XGBoostExplainerが何をやっているか調べる（２．可視化プロセスを眺める）

R R package interpretability xgboost

目的

今回は、xgboostExplainerによって、xgboostのモデルと予測結果から何が取り出され、どう捌かれているかにフォーカスして追いかける。

関連シリーズ

  1. とりあえず使ってみる
  2. 予測結果の可視化プロセスをstep-by-stepで実行する（この記事）
  3. 予測結果を分解再構成するプロセスをstep-by-stepで実行する
  4. 学習したxgboostのルール抽出をstep-by-stepで実行する

予測結果の可視化プロセスをstep-by-stepで眺める

showWaterfall(..., type = "binary")の中身を抜き書きしながら、都度、何が取り出されているか見ていく。*1

準備

XGBモデルの学習と予測

xgboostExplainerのマニュアルにあるexampleからコピペ。

require(tidyverse)
library(xgboost)
library(xgboostExplainer)

set.seed(123)

data(agaricus.train, package='xgboost')

X = as.matrix(agaricus.train$data)
y = agaricus.train$label
table(y)
train_idx = 1:5000

train.data = X[train_idx,]
test.data = X[-train_idx,]

xgb.train.data <- xgb.DMatrix(train.data, label = y[train_idx])
xgb.test.data <- xgb.DMatrix(test.data)

param <- list(objective = "binary:logistic")
xgb.model <- xgboost(param =param,  data = xgb.train.data, nrounds=3)

可視化の手続き

overview

あるインスタンスの予測結果を可視化する手順は：

  1. 学習したxgboostのモデルから予測ルールを抽出する
  2. showWaterfall()のなかで
    1. 指定したインスタンスの予測結果を予測ルールから分解再構成する
    2. 分解再構成した予測結果をwatarfall chartで可視化する

なお、

  • buildExplainer()がどうやってモデルから予測ルールを抽出しているか
  • explainPredictions()がどうやって分解再構成するか

については今回は触れない。

学習したxgboostのモデルから予測ルールを抽出する

buildExplainer()が抽出した予測ルール(ノード)を眺める。

library(xgboostExplainer)

explainer = buildExplainer(xgb.model,xgb.train.data, type="binary", base_score = 0.5, trees = NULL)

今回はルールの数が多いので、一度も登場しないものを除外してみる：

nonzero.cols <- abs(explainer) %>% 
  colSums() %>% 
  is_greater_than(0.0) %>% 
  which()

explainer %>% 
  select(nonzero.cols %>% rev()) %>% 
  set_colnames(
    colnames(.) %>% 
      str_trunc(width=10, side="left"))
#>     tree leaf   intercept  ...r=green ...g=silky ...e=broad  odor=none
#>  1:    0    2 -0.11061173  0.00000000  0.0000000  0.0000000  0.0000000
#>  2:    0    7 -0.11061173 -0.02193993  0.0000000 -0.1919848  0.0000000
#>  3:    0    8 -0.11061173  1.13508088  0.0000000 -0.1919848  0.0000000
#>  4:    0   10 -0.11061173  0.00000000  0.0000000  0.6632849  0.1868594
#>  5:    0   12 -0.11061173  0.00000000  0.8995779  0.6632849 -0.6576614
#>  6:    0   14 -0.11061173  0.00000000  0.0000000  0.6632849  0.1868594
#>  7:    0   15 -0.11061173  0.00000000 -0.1528694  0.6632849 -0.6576614
#>  8:    0   16 -0.11061173  0.00000000 -0.1528694  0.6632849 -0.6576614
#>  9:    0   17 -0.11061173  0.00000000  0.0000000  0.6632849  0.1868594
#> 10:    0   18 -0.11061173  0.00000000  0.0000000  0.6632849  0.1868594
#> 11:    1    2 -0.08586974  0.00000000  0.0000000  0.0000000  0.0000000
#> 12:    1    7 -0.08586974 -0.01726586  0.0000000 -0.1483337  0.0000000
#> 13:    1    8 -0.08586974  0.88295840  0.0000000 -0.1483337  0.0000000
#> 14:    1   10 -0.08586974  0.00000000  0.0000000  0.5101908  0.1433645
#> 15:    1   12 -0.08586974  0.00000000  0.7008943  0.5101908 -0.5018480
#> 16:    1   13 -0.08586974  0.00000000  0.0000000  0.5101908  0.1433645
#> 17:    1   14 -0.08586974  0.00000000  0.0000000  0.5101908  0.1433645
#> 18:    1   15 -0.08586974  0.00000000 -0.1208858  0.5101908 -0.5018480
#> 19:    1   16 -0.08586974  0.00000000 -0.1208858  0.5101908 -0.5018480
#> 20:    2    2 -0.07436510  0.00000000  0.0000000  0.0000000  0.0000000
#> 21:    2    7 -0.07436510 -0.01523278  0.0000000 -0.1291144  0.0000000
#> 22:    2    8 -0.07436510  0.76272457  0.0000000 -0.1291144  0.0000000
#> 23:    2   10 -0.07436510  0.00000000  0.0000000  0.4407547  0.1238637
#> 24:    2   12 -0.07436510  0.00000000  0.5980809  0.4407547 -0.4287505
#> 25:    2   13 -0.07436510  0.00000000  0.0000000  0.4407547  0.1238637
#> 26:    2   14 -0.07436510  0.00000000  0.0000000  0.4407547  0.1238637
#> 27:    2   15 -0.07436510  0.00000000 -0.1059506  0.4407547 -0.4287505
#> 28:    2   16 -0.07436510  0.00000000 -0.1059506  0.4407547 -0.4287505
#>     tree leaf   intercept  ...r=green ...g=silky ...e=broad  odor=none
#>      odor=foul  odor=anise  ...=almond  ...bruises  ...=yellow
#>  1:  0.7088975  0.00000000  0.00000000  0.00000000  0.00000000
#>  2: -0.2745896  0.00000000  0.00000000  0.00000000  0.00000000
#>  3: -0.2745896  0.00000000  0.00000000  0.00000000  0.00000000
#>  4: -0.2745896  0.00000000  0.00000000  0.00000000 -1.00780012
#>  5: -0.2745896  0.00000000  0.00000000  0.00000000  0.00000000
#>  6: -0.2745896  0.00000000 -1.02528500  0.00000000  0.06468987
#>  7: -0.2745896  0.00000000  0.00000000 -0.05144537  0.00000000
#>  8: -0.2745896  0.00000000  0.00000000  0.93244731  0.00000000
#>  9: -0.2745896  0.03208427  0.03399723  0.00000000  0.06468987
#> 10: -0.2745896 -1.04934438  0.03399723  0.00000000  0.06468987
#> 11:  0.5493453  0.00000000  0.00000000  0.00000000  0.00000000
#> 12: -0.2125787  0.00000000  0.00000000  0.00000000  0.00000000
#> 13: -0.2125787  0.00000000  0.00000000  0.00000000  0.00000000
#> 14: -0.2125787  0.00000000 -0.78526446  0.00000000  0.00000000
#> 15: -0.2125787  0.00000000  0.00000000  0.00000000  0.00000000
#> 16: -0.2125787  0.05522851  0.05139002  0.00000000  0.00000000
#> 17: -0.2125787 -0.83485874  0.05139002  0.00000000  0.00000000
#> 18: -0.2125787  0.00000000  0.00000000 -0.04271214  0.00000000
#> 19: -0.2125787  0.00000000  0.00000000  0.74060173  0.00000000
#> 20:  0.4766099  0.00000000  0.00000000  0.00000000  0.00000000
#> 21: -0.1841252  0.00000000  0.00000000  0.00000000  0.00000000
#> 22: -0.1841252  0.00000000  0.00000000  0.00000000  0.00000000
#> 23: -0.1841252  0.00000000 -0.67413428  0.00000000  0.00000000
#> 24: -0.1841252  0.00000000  0.00000000  0.00000000  0.00000000
#> 25: -0.1841252  0.04896816  0.04534281  0.00000000  0.00000000
#> 26: -0.1841252 -0.71778146  0.04534281  0.00000000  0.00000000
#> 27: -0.1841252  0.00000000  0.00000000 -0.03984976  0.00000000
#> 28: -0.1841252  0.00000000  0.00000000  0.63572177  0.00000000
#>      odor=foul  odor=anise  ...=almond  ...bruises  ...=yellow

それぞれの木*2のなかでleafにたどり着くためのルールの組み合わせと、更新される予測の量がわかる。

指定したインスタンスの予測結果を予測ルールから分解再構成する

指定したインスタンスの予測結果を、explainPredictions()が再構成した結果(breakdown)を眺める*3。

# showWaterfall(xgb.model, explainer, xgb.test.data, test.data,  2, type = "binary")

DMatrix = xgb.test.data
data.matrix = test.data
idx = 2
type = "binary"
threshold = 1e-04
limits = c(NA, NA)

breakdown = explainPredictions(xgb.model, explainer, slice(DMatrix, as.integer(idx)))

ルールが多いので非ゼロのものだけ眺める。

breakdown_summary = as.matrix(breakdown)[1, ]
breakdown_summary[which(abs(breakdown_summary) > 0.0)]
#> cap-color=yellow      odor=almond       odor=anise        odor=foul 
#>       0.06468987       0.13073006       0.13628094      -0.67129347 
#>        odor=none  gill-size=broad        intercept 
#>       0.45408751       1.61423045      -0.27084657

今回は、objective = "binary:logistic"なので、予測値(対数オッズ)は逆ロジット変換により予測結果(クラス所属確率)に変換される

(weight = rowSums(breakdown))
#> [1] 1.457879

(pred = 1/(1 + exp(-weight)))
#> [1] 0.811208

分解再構成した予測結果を可視化する

プロットの方針は以下の通り。

  1. ベースライン(Intercept)を先頭に表示、残りをインパクト(貢献量)が大きい順に表示
  2. インパクトが微小(< threshold)のルールは、その他(other_impact)にまとめる
data_for_label = data.matrix[idx, ]
i = order(abs(breakdown_summary), decreasing = TRUE)
breakdown_summary = breakdown_summary[i]
data_for_label = data_for_label[i]

intercept = breakdown_summary[names(breakdown_summary) == "intercept"]
data_for_label = data_for_label[names(breakdown_summary) != "intercept"]
breakdown_summary = breakdown_summary[names(breakdown_summary) != "intercept"]

thresholdの値はオプション指定で変更でき、インパクトの大きなルールだけに絞り込んで表示できる。やたら細かいルールがいっぱい生えちゃったとかでもない限り*4thresholdはデフォルトのままで良さそう。

i_other = which(abs(breakdown_summary) < threshold)
other_impact = 0
if (length(i_other > 0)) {
  other_impact = sum(breakdown_summary[i_other])
  names(other_impact) = "other"
  breakdown_summary = breakdown_summary[-i_other]
  data_for_label = data_for_label[-i_other]
}
if (abs(other_impact) > 0) {
  breakdown_summary = c(intercept, breakdown_summary, other_impact)
  data_for_label = c("", data_for_label, "")
  labels = paste0(names(breakdown_summary), " = ", data_for_label)
  labels[1] = "intercept"
  labels[length(labels)] = "other"
} else {
  breakdown_summary = c(intercept, breakdown_summary)
  data_for_label = c("", data_for_label)
  labels = paste0(names(breakdown_summary), " = ", data_for_label)
  labels[1] = "intercept"
}

breakdown_summary
#>        intercept  gill-size=broad        odor=foul        odor=none 
#>      -0.27084657       1.61423045      -0.67129347       0.45408751 
#>       odor=anise      odor=almond cap-color=yellow 
#>       0.13628094       0.13073006       0.06468987

頑張って並び替えた。

watarfall chartによる予測結果の描画

算出した値の出力。getinfoの箇所はラベルの実名か何かを取ろうとしてる？　キノコのデータだとスキップされる。

if (!is.null(getinfo(DMatrix, "label"))) {
  cat("\nActual: ", getinfo(slice(DMatrix, as.integer(idx)), "label"))
}
cat("\nPrediction: ", pred)
#> 
#> Prediction:  0.811208
cat("\nWeight: ", weight)
#> 
#> Weight:  1.457879
cat("\nBreakdown")
#> 
#> Breakdown
cat("\n")
print(breakdown_summary)
#>        intercept  gill-size=broad        odor=foul        odor=none 
#>      -0.27084657       1.61423045      -0.67129347       0.45408751 
#>       odor=anise      odor=almond cap-color=yellow 
#>       0.13628094       0.13073006       0.06468987

予測結果(クラス所属確率)で表示するための工夫をする。inverse_logit_labelsとlogitは、y軸を対数オッズからクラス所属確率に読み替えるための関数。*5

inverse_logit_trans <- scales::trans_new("inverse logit", transform = plogis, inverse = qlogis)

inverse_logit_labels = function(x) {
  return(1/(1 + exp(-x)))
}

logit = function(x) {
  return(log(x/(1 - x)))
}

ybreaks <- logit(seq(2, 98, 2)/100)

waterfalls::waterfall(
  values = breakdown_summary,
  rect_text_labels = round(breakdown_summary, 2),
  labels = labels, 
  total_rect_text = round(weight, 2),
  calc_total = TRUE,
  total_axis_text = "Prediction") + 
  scale_y_continuous(labels = inverse_logit_labels,
                     breaks = ybreaks, 
                     limits = limits) + 
  theme(axis.text.x = element_text(angle = 45, hjust = 1))

f:id:kato-satoshi-0:20181212131040p:plain

waterfalls::waterfall()は、CRANのパッケージをそのまま利用する。

cran.r-project.org

次回は、explainPredictions()が、どのような手続きで指定したインスタンスの予測結果を分解再構成しているのか詳細に見ていく。

*1:なお、この記事以降では、binary:logisticを扱って進めるが、reg:linearと本質的には変わらない。前者がわかれば後者は相対的にシンプルな手続きであり自然に理解できる。

*2: nrounds = 3 なので、決定木（０番のtree）と、対応するエラーを予測する木（１と２）

*3:インスタンスはベクトルで複数指定できるが、先頭のインスタンスだけがプロット時に使用される

*4:tree depthのチューニングに失敗してoverfitしてそうではあるし、一つのインスタンスの説明用途としては失敗しているともいえる。

*5:inverse_logit_trans`はコメントアウトしても動作する。レガシーだろうか？

XGBoostExplainerが何をやっているか調べる（１．とりあえず使う）

R R package interpretability xgboost

目的

XGBoostの予測を分解するツールXGBoostExplainerは、あるインスタンスについて得られたXGBoostによる予測結果が、どのように構成されているか可視化してくれる。

f:id:kato-satoshi-0:20181212125239p:plain

コンセプトとしては、randomforestにおけるforestfloorと同じく、feature contributionを算出する。ターゲット集団の変数の感度分析に使うのではなく*1、個々のインスタンスのxgboostによる予測結果の説明をWaterfall Chartで可視化してくれるのが特徴。

なお、同様のWaterfall Chartによる説明は、そのほかの手法についても提供されているようだ。

lightgbmの予測結果に適用してくれるパッケージ

lm/glmの予測結果に適用してくれるパッケージ

探索的なデータ分析に使うだけならおおむね問題ないと思うが、具体的に何をやっているか説明しようとして困った。論文などの詳細な資料も見つけられなかったため、XGBoostExplainerの実装を追いかけて、何をやっているか調べた。

関連シリーズ

  1. とりあえず使ってみる
  2. 予測結果の可視化プロセスをstep-by-stepで実行する（この記事）
  3. 予測結果を分解再構成するプロセスをstep-by-stepで実行する
  4. 学習したxgboostのルール抽出をstep-by-stepで実行する

参考

開発元の紹介記事

medium.com

とりあえず使ってみる

すでに日本語の記事がある。

qiita.com

xgboostExplainerのマニュアルにあるexampleからコピペを眺める。

インストール

本家の記事に従ってgithubからインストール

install.packages("devtools") 
library(devtools) 
install_github("AppliedDataSciencePartners/xgboostExplainer")

XGBモデルの学習と予測

今回はxgboostパッケージ付属のサンプルデータで、定番の食えるキノコと毒キノコの2値分類。細かいチューニングは、必要に応じてautoxgbあたりでチューニングするとよいが、今回は省略。

library(xgboost)
require(tidyverse)
library(xgboost)
library(xgboostExplainer)

set.seed(123)

data(agaricus.train, package='xgboost')

X = as.matrix(agaricus.train$data)
y = agaricus.train$label
table(y)
train_idx = 1:5000

train.data = X[train_idx,]
test.data = X[-train_idx,]

xgb.train.data <- xgb.DMatrix(train.data, label = y[train_idx])
xgb.test.data <- xgb.DMatrix(test.data)

param <- list(objective = "binary:logistic")
xgb.model <- xgboost(param =param,  data = xgb.train.data, nrounds=3)
# 
# col_names = colnames(X)
# 
# pred.train = predict(xgb.model,X)
# nodes.train = predict(xgb.model,X,predleaf =TRUE)
# trees = xgb.model.dt.tree(col_names, model = xgb.model)

個別の予測結果の可視化

xgboostExplainerのマニュアルにあるexampleのコピペ（つづき）。高度にwrapされているためわずか3行でstep-by-stepが完了する。

STEP.1. 学習済みXGBモデルからルールセット（leafまでのパス）を列挙してテーブル化

base_scoreオプションはxgboostのオプションそのままで、ターゲット集団のクラス不均衡を表す事前確率。すなわち正例：負例＝300:700を仮定できる対象であれば、base_score = 0.3となる(デフォルトは1:1を表す0.5)。

library(xgboostExplainer)

explainer = buildExplainer(xgb.model,xgb.train.data, type="binary", base_score = 0.5, trees = NULL)
#> 
#> Creating the trees of the xgboost model...
#> Getting the leaf nodes for the training set observations...
#> Building the Explainer...
#> STEP 1 of 2
#> 
#> Recalculating the cover for each non-leaf... 
#> 
  |=================================================================| 100%
#> 
#> Finding the stats for the xgboost trees...
#>                                                                        
  |=================================================================| 100%
#> 
#> STEP 2 of 2
#> 
#> Getting breakdown for each leaf of each tree...
#>                                                                 
  |=================================================================| 100%
#> 
#> DONE!

STEP.2. Get multiple prediction breakdowns from a trained xgboost model

マニュアルには step2とあるのだが、実はパッケージを使うだけならスキップできてしまう。

STEP.3. 予測対象(インスタンス)に適用される各treeのパスを集計して可視化

2値分類(binary:logistic)では、片側のクラスに属する確率p（左軸の数値）のロジット（対数オッズ；棒グラフ中の数値）が足し合わされている様子を表示する。

showWaterfall(xgb.model, explainer, xgb.test.data, test.data,  2, type = "binary")
#> 
#> 
#> Extracting the breakdown of each prediction...
#> 
 |=================================================================| 100%
#> 
#> DONE!
#> 
#> Prediction:  0.811208
#> Weight:  1.457879
#> Breakdown
#>        intercept  gill-size=broad        odor=foul        odor=none 
#>      -0.27084657       1.61423045      -0.67129347       0.45408751 
#>       odor=anise      odor=almond cap-color=yellow 
#>       0.13628094       0.13073006       0.06468987

f:id:kato-satoshi-0:20181212131040p:plain

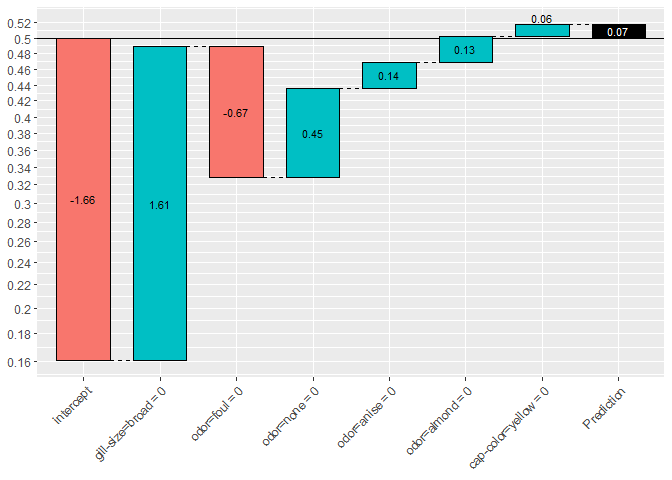
(参考) binary:logisticの場合、base_scoreで設定した事前確率は ベースラインとしてinterceptに反映される。下記の例ではinterceptだけが下がっていることに注目されたい。

explainer = buildExplainer(xgb.model,xgb.train.data, type="binary", base_score = 0.2, trees = NULL)

showWaterfall(xgb.model, explainer, xgb.test.data, test.data,  2, type = "binary")
#> 
#> 
#> Extracting the breakdown of each prediction...
#> 
  |=================================================================| 100%
#> 
#> DONE!
#> 
#> Prediction:  0.5178885
#> Weight:  0.07158444
#> Breakdown
#>        intercept  gill-size=broad        odor=foul        odor=none 
#>      -1.65714093       1.61423045      -0.67129347       0.45408751 
#>       odor=anise      odor=almond cap-color=yellow 
#>       0.13628094       0.13073006       0.06468987

f:id:kato-satoshi-0:20181212131004p:plain

次回は、xgboostExplainerにより、xgboostのモデルと予測結果から何が取り出され、どう捌かれているかだけを詳細に見ていく。

*1:XGBoostExplainerの開発者による記事では、感度分析も行っている

［感想］『自然科学研究のためのR入門』

まずは、本書を御恵贈いただき、あらためて著者に感謝したい。あくまで感想文として、この本を教科書として、同僚（特に若い方）やカウンターパートと仕事を共有するうえで、自分ならどのようなポイントに注意するかに焦点を絞ってコメントしたい*1。

全体

対象としない読者

  • ご自身ではデータ分析とレポート作成をしないポジションのかた
  • このご時世でも『研究の再現性は不要』と思ってるひと
  • 『再現可能なレポート』について精通しているRユーザー
  • Rによるデータ分析自体の習得を目指しているかた

上記以外は必読。ただし、研究責任者としてご自身ではデータ分析に従事しない立場であっても、こうした技術的に解決できる枠組みを検討せず、対策を講じていないままという態度は無責任といえよう。

www.kyoritsu-pub.co.jp

測定した、シミュレーションした、あるいはカウンターパートから預かったデータを分析するのが、（特に自然科学の）研究者の日常的な活動のひとつ*2。

言い尽くされていることではあるが、報告した結果を元のデータから再現できることは、データ分析者にとっての最良の自衛手段であり義務でもある。その立場と目的にたって、本書は研究者や学生が『再現可能なレポート』を書くために、必要なステップと今の技術を最速で習得するための一冊になっている *3。

COI

著書をご恵投いただく程度には交流がある。

1章：RmarkdownとRstudioを使う

Rによるデータ分析結果を報告するという目的上、報告以前のデータ分析の知識はある程度は持っていることが前提。

引用文献リストの自動取り込み方法も触れられている。引用文献リストの掲載がひとつもないレポートは研究報告には値しないので*4*5、この作業の定型化と省力化は研究報告の作成時には非常に重要なポイントとなる。類書ではあまり最初に出てこないが、本書ではこれが１章でカバーされており、ツールの選定・検討中の研究者には嬉しい。

本書の特色として、各章にsession_info()の出力が付けられている。報告相手が別の環境でレポートの再現を試みることを想定して、分析環境の情報共有も重要なポイントといえる。 自分以外の人に、結果（あるいはデータ分析がうまく行かない）を相談したり、報告内容を再現してもらう際にしばしばトラップとなる*6。

2,3,4章：統計モデリング、実験計画法と分散分析を使った分析とレポーティング

これらの各章では、データの分析をstep-by-stepで実施しながら、一通りの分析が終わった時点でレポートが出来上がっているという流れになっており、Rmarkdownの嬉しさが最大限に発揮されるポイントのひとつといえるだろう。

これ以降の章では、一連の分析風景を追いかけてくれているので具体的なイメージを持ちやすい。 機械学習などによる分析や自身で提案した新しい分析手法を報告する際にも、既存の方法をベースラインとした対比が必要となる*7。 データ分析に際して、どのような順番でどのような方法でアプローチしていくか、あるいはそれぞれの分析において着目すべきポイントや勘所が随所にちりばめられており、著者の経験に基づいた実践的な知識の一端に触れることができるのも楽しい。

5章：機械学習（など）を使った分析のレポーティング

冒頭でごく簡単に、Bioconductorからのパッケージの導入にも触れている。本書の読者には、実験から解析までこなすバイオインフォマティシャンも多く想定され、分析風景がより身近になるのではないだろうか。

再現性の観点から、欲を言えば、機械学習の方法には乱数を利用するものも多いため*8、set.seed()で乱数を固定する方法は紹介されても良かったかなと思う *9 *10。

最近は、初期検討として機械学習の各種手法を横並びに比較をすることも多く、メタフレームワークのひとつであるcaretを使った学習パラメタのチューニング・性能評価と比較方法の紹介はありがたい *11 *12。

また、xgboostのパラメータチューニングについては、全自動でやってくれるautoxgboostもあるので薦めておきたい。

kato-kohaku-0.hatenablog.com

AUCROCによるパフォーマンスの比較について

ROCが三角形になっていて気になった*13。これは予測ラベルを直接投入しているためと思われるが、各症例の予測値や検査値をもとにROCをみながらカットオフの検討をしてる業界などでは、この図で報告すると戸惑われる可能性がある *14。

たとえば、random forestのラベルの得票率とlassoの回帰の値をそれぞれ投入して、両者を比較したらよかったのではないかと思う *15。

require(randomForest)
require(glmnet)
require(pROC)

data(spam, package = "kernlab")
# glimpse(spam)

X <- spam[, -NCOL(spam)]
y <- as.factor(spam[,  NCOL(spam)])

train <- sample(1:NROW(spam), NROW(spam) * 0.7)
test  <- setdiff(1:NROW(spam), train)

# train learner + predict test with random forest
rf <- randomForest(X[train, ], y[train], ntree=500)
pred.rf <- predict(rf, X[test, ], type="prob")
head(pred.rf)
#>    nonspam  spam
#> 4    0.026 0.974
#> 24   0.296 0.704
#> 30   0.082 0.918
#> 32   0.078 0.922
#> 33   0.236 0.764
#> 34   0.844 0.156

# tune-train learner + predict test with lasso
cv <- cv.glmnet(x = as.matrix(X[train, ]), y = as.numeric(y[train]))
lasso <- glmnet(x = as.matrix(X[train, ]), y = as.numeric(y[train]), lambda = cv$lambda.1se, alpha = 1)
pred.lasso <- predict(lasso, as.matrix(X[test, ]))
head(pred.lasso)
#>          s0
#> 4  1.481061
#> 24 1.529340
#> 30 1.899370
#> 32 1.652855
#> 33 1.592823
#> 34 1.532178

# prot ROC
roc.rf <- roc(response = y[test],             predictor = pred.rf[,1])
roc.la <- roc(response = as.numeric(y[test]), predictor = c(pred.lasso))

mt <- sprintf("RF(red) vs lasso(blue) = %.3f vs =%.3f",auc(roc.rf),auc(roc.la))
plot.roc(roc.rf, col = "red",  main = mt)
plot.roc(roc.la, col = "blue", add = TRUE)

f:id:kato-satoshi-0:20181013115315p:plain

6章：集大成

この章では、レポートの提出を強く意識する*16 報告相手に次第では、コード部分や処理途中の出力などはノイズでしかなく、場合によってはレポートそのものを見てもらえないこともある *17。重要なポイントと思った。

結論：（Rで）データ分析をしている研究者には必携の書

  • 報告の必要がなくても、手元の分析結果をレポートの形で残す習慣を身に着けたい
  • R以外で分析をするユーザーを対象とした書籍が出てくれると良い。

www.kyoritsu-pub.co.jp

*1:献本を遣り取りする文化から転職して既に長いため、書評のようにきちんと精査したものではないことは、ご容赦されたい。

*2:純粋な理論系は違うかもしれないが..

*3:必要最低限の情報提供にとどめることで、常々忙しい忙しいとか多言する研究者に取捨選択をさせないスタイルになっているが、各章末に発展内容への適切なガイドを付けることでカバーされている

*4:少なくとも自然科学の研究者にとって

*5:ただの作業記録やポエムならともかく

*6:報告書の作成時には見落としがちであるが、OSが違ったり、分析に必要なパッケージが入ってなかったり、使っているパッケージがバージョンアップでオプションの指定方法が変わったり、出力されるデータの構造が変わったりすることがある

*7:情報学系なら事情が異なるかもしれないが、自分の業界では査読で必ず突っ込まれる

*8:例えば本書でも取り上げられているrandom forestなど

*9:特に初学者が再現を試みたときに結果の数字が元のテキストと違っていると戸惑うことが多い

*10:一意な乱数に固定することで、報告対象にチャンピオンデータを誘導したりネガティブな結果を隠蔽しかねない悪用や弊害があるのは承知している

*11:自分はmlRユーザーなのでcaretはあまり常用してないけど、事情はそれほど変わらないだろう

*12:ついでながら、expand.grid()は、caretじゃなくてbaseの関数だけど、実践的には困ることはないだろう

*13:情報系の論文では見るので、目的に応じるのだと思う

*14:誰に報告するかといった業界や事情の違いがあるので、あくまで個人的な体験に基づく

*15:手元のデータでパパっとやったので、本書のデータでの解析例ではないことはご容赦されたい

*16:include=FALSE や echo=FALSE といったチャンクオプションを使いながら、適宜、隠蔽する方法が示されており、分析者が手元で再現できれば良い、あるいは、付録として分けるといった説明がされている。

*17:このあたりは、どういう相手かに応じて分ける必要がある